Commonly used in networks as MobileNet and Xception, the depthwise separable convolutions consists of two steps: depthwise convolutions and 1×1 convolutions.
Standard convolution
Before describing the depthwise separable convolution, it is worth revisiting the typical convolution. For a concrete example, let’s say an input layer of size 7×7×3 (height×width×channels), and 128 filters of size 3×3×3, after applying one filter, the output layer is of size 5×5×1 (only 1 channel), and grouped up with the 128 filters, 5×5×128.
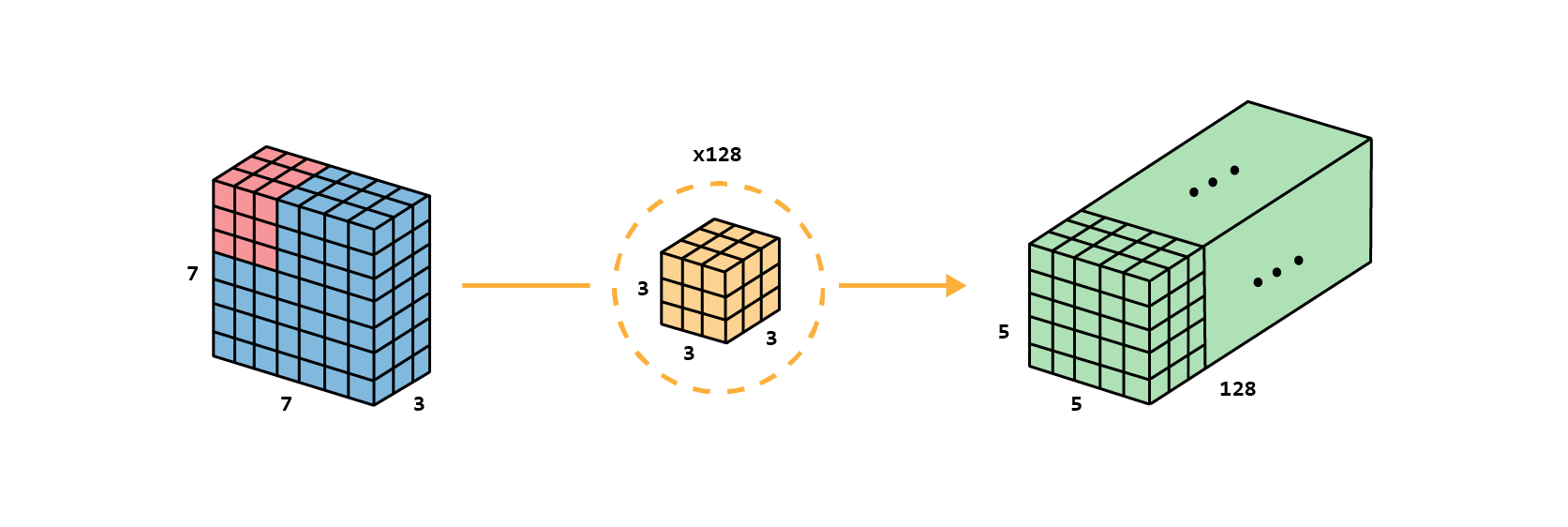
# Input volume with depth 3 and outputs 128 kernels
# Uses 3×3 convolutional kernel
conv_layer = nn.Conv2d(in_channels=3, out_channels=128, kernel_size=3)Depthwise Separable Convolutions
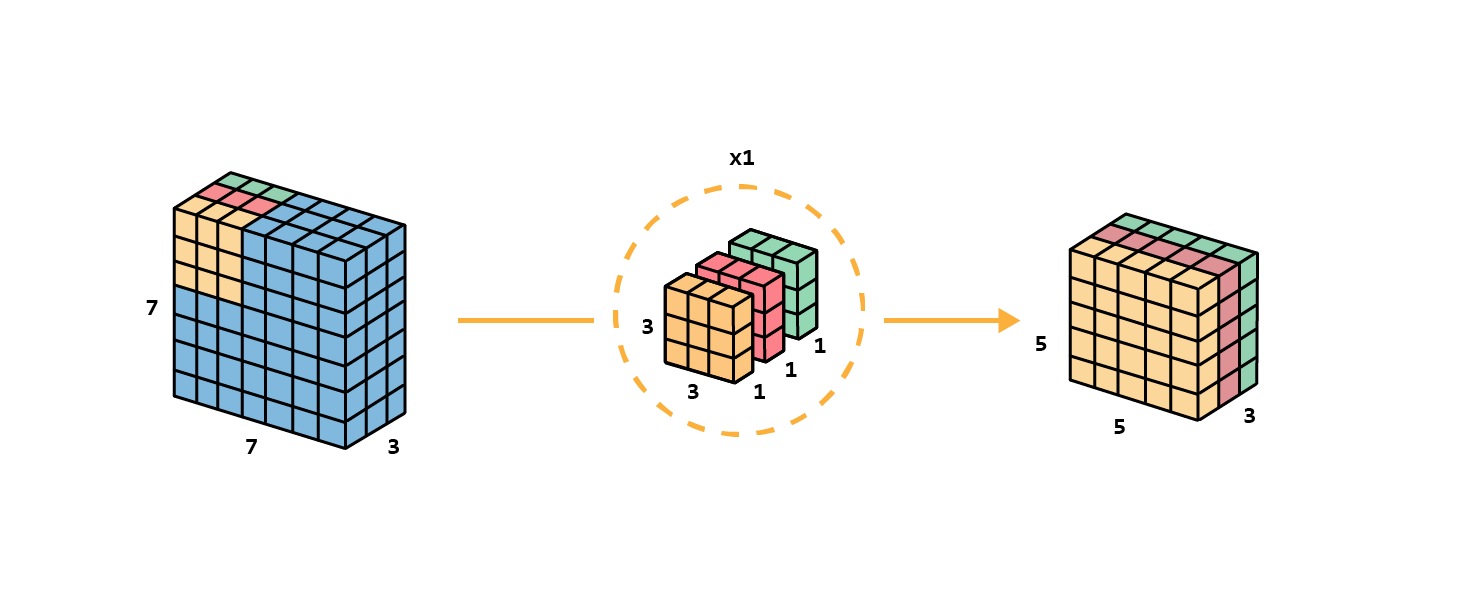
Let’s see how we can achieve the same transformation as the standard convolution.
We first apply depthwise convolution to the input layer. Instead of using a single filter of size 3×3×3, we will use 3 kernels separately. Each filter has a size of 3×3×1, each kernel convolves with 1 channel of the input layer (1 channel only, not all channels!). Each such convolution, in the example, will provide a map of size 5×5×1, and we will stack them to create a 5×5×3 image. We shrunk the spatial dimension, but the depth is still the same as before.
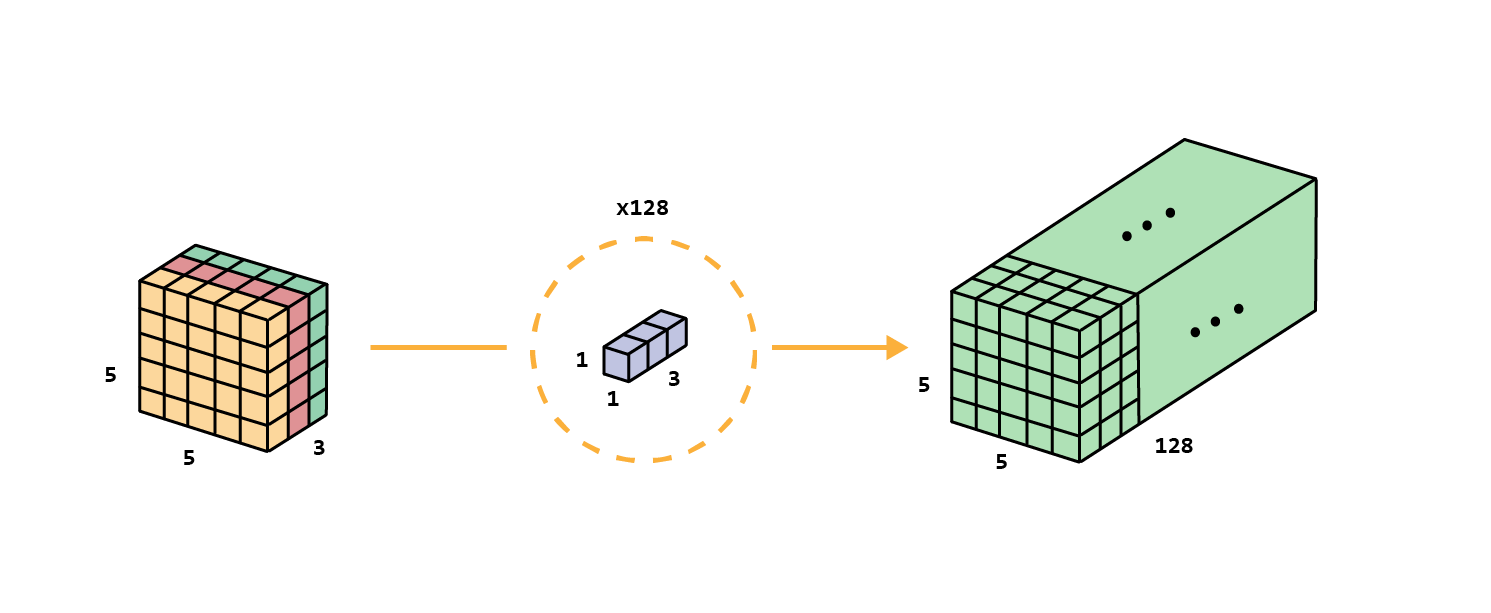
Then, it’s time for the second step, extend the depth by applying 1×1 convolutions, as many as the depth we want to achieve, as for the example 128 filters.
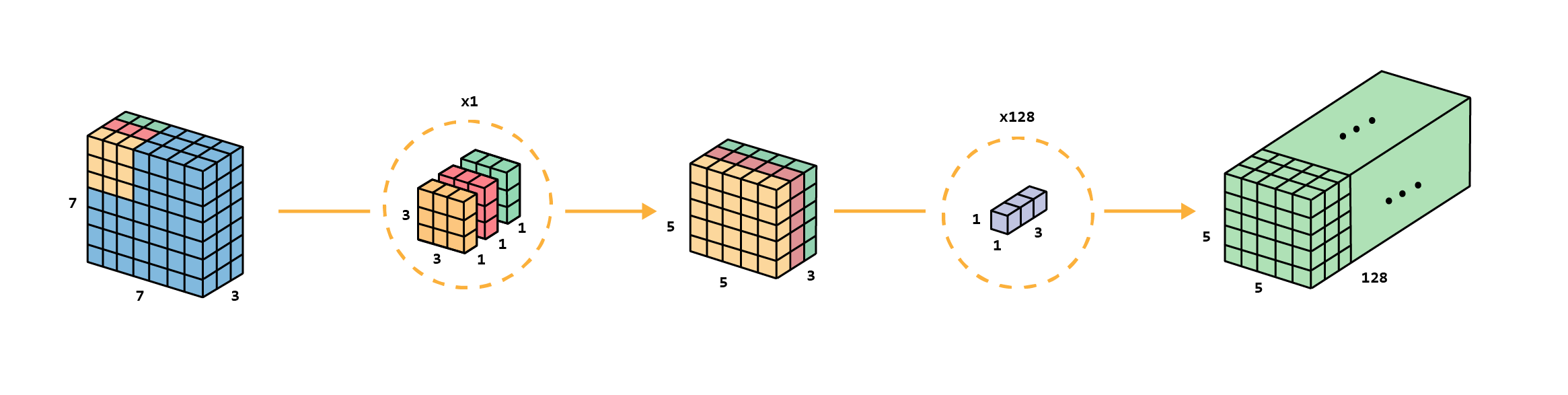
With these steps, we also (as in the standard convolution) transform the input layer 7×7×3 into the output layer 5×5×128 as for the standard convolution. The overall process of the depthwise separable convolution would be:
# Define depthwise separable convolutional layer
# Note how we use the groups parameter: At groups equals to in_channels,
# each input channel is convolved with its own set of filters
depthwise_conv_layer = nn.Conv2d(in_channels=3, out_channels=3, kernel_size=3, groups=3)
pointwise_conv_layer = nn.Conv2d(in_channels=3, out_channels=128, kernel_size=1)The advantage of doing depthwise separable convolutions is the efficiency. One needs much less operations for depthwise separable convolutions compared to standard convolutions.
Meanwhile for the standard convolutions we need to move 128 filters with dimensionality 3×3×3 around the input 5×5 times, i.e., 86400 multiplications, the depthwise separable convolution uses 3 kernels 3×3×1 that moves 5×5 times, and after that, 128 filters of dimensionality 1×1×3 that moves 5×5 times over the previous output, i.e., 9600 multiplications, only about the 12% of the cost of the standard convolution.
