TF-IDF & BM25 Explained

This post is a summary of the Understanding TF-IDF and BM-25 article by KMW Technology. Here we going straight to the point, to use this post as a quick reminder of how these algorithms work.

These algorithms are used to rank documents based on a query. They are used in search engines, recommendation systems, etc. Mainly they reward the relevance of a query with respect to a document. When applied to all documents, we can known which documents are more relevant to a query.

TF-IDF

Assumptions

The TF-IDF algorithm is based on two concepts:

• Term Frequency (TF): The number of times a term appears in a document. It is supposed that the more times a document contains a term, the more likely it is to be about that term. Can be seen as a proxy for the relevance of a term in a document.
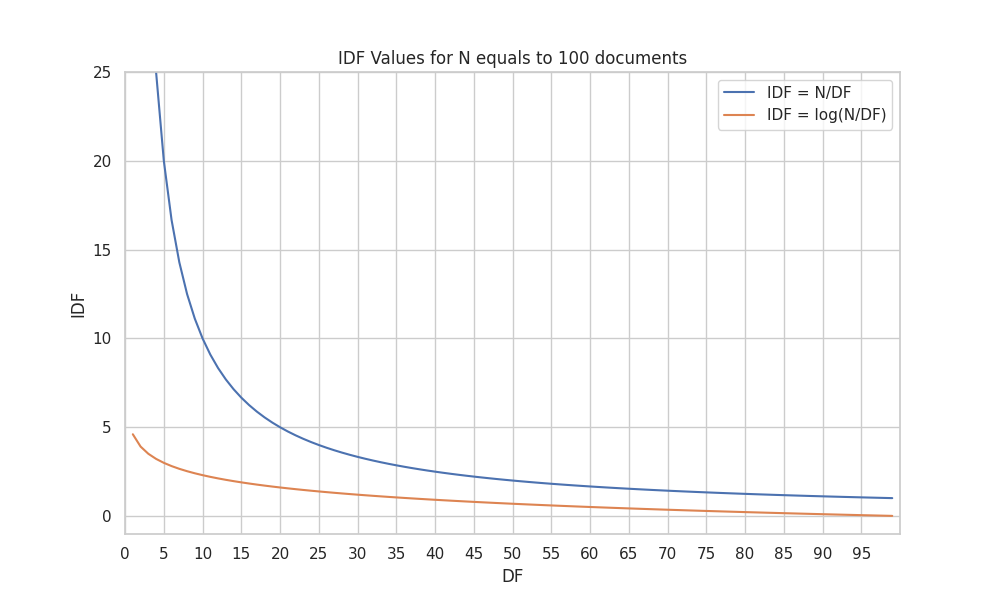
• Inverse Document Frequency (IDF): The number of documents that contain a term by the total number of documents, scaled logarithmically. All terms are not equally important, imagine filler words like “the”, “a”, “an”, etc. We need to judge the rarity of the terms. To do so we account for the number of documents that contain a term from the total number of documents. But there is a problem: imagine that we have 100 documents and a term like “elephant” appears in 1 document while the term “giraffe” occurs in 2 documents, if we simply divide the number of documents that contain a term by the total number of documents, we will get that “elephant” is the double (100 points) as important as “giraffe” (50 points). But we know that they are pretty similarly rare. To solve this problem we use the logarithm of the fraction. Check the following graph to see how the logarithm of the fraction scales the values.

Formula

The TF-IDF formula is the following:

$\text{TF-IDF}(t, d) = \text{TF}(t, d) \times \text{IDF}(t)$

Where $t$ is a term and $d$ is a document. We can expand the formula as follows:

$\text{TF-IDF}(t, d) = \text{counts of t in d} \times \log{\frac{\text{total number of documents}}{\text{number of documents containing t}}}$

Problems

• Term Frequency: The TF is not normalized by the length of the document. Longer documents are given an unfair advantage over shorter ones because they have more space to include more occurrences of a term, even though they might not be more relevant to the term.

BM25

The BM25 algorithm is based on the TF-IDF algorithm, but trying to solve some of its problems.

Assumptions

• Saturation: The relevance of a term in a document saturates after a certain point. Is it really twice as relevant a document with 200 occurrences of a term than a document with 100 occurrence? We need that the term frequency contribution increases fast when the term frequency is small and then increases more slowly. To achive this we will use a small trick: modify the term frequency with $\frac{TF}{TF+k}$, where $k$ is a hyperparameter. This way the term frequency contribution will always saturate to 1 for large values of $TF$, while for small values of $TF$ it will increase moderately fast. Additionaly, a side-effect of this saturation is that we end up rewarding complete matches over partial ones. For example, given a query searching for “cat and dog” and $k=1$, a document with both ocurrences of “cat” and “dog” will be more relevant than a document with only two ocurrences of “cat” or “dog”, as the values will not be so predominant.

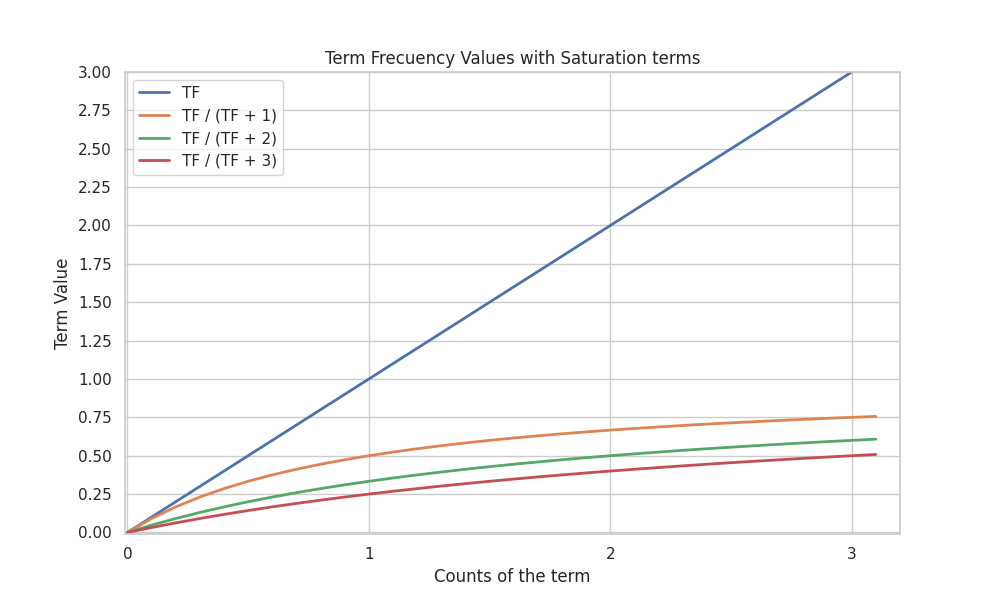
• Document Length: If a document is very short and contains an occurrence of a term, like “cat”, that’s a very strong signal that the document is about cats. But if a document is very long and only contains one occurrence of a “cat”, probably the document is not about cats. To solve this problem we need to reward the matches in short documents more than the matches in long documents. The first step we need to do is to decide what is a short and a long document. To do so we will use the average document length of the corpus. Going back to our saturation formula, $\frac{TF}{TF+k}$, we can adjust the $k$ hyperparameter to account for the document length. If we multiply $k$ by the ratio between the document length and the average document length ($\frac{doc\_length}{avg\_doc\_length}$), we will get a value that will be smaller than 1 for short documents and larger than 1 for long documents. This way we will reward the matches in short documents more than the matches in long documents, as lower values of $k$ will be used for short documents than for long documents. Building on top of this, maybe for our problem is not so important the document length, so to control the importance of the document length we will use a hyperparameter $b$, between 0 and 1, that will be multiplied by the ratio between the document length and the average document length. This hyperparameter is introduced as $1-b+b\frac{doc\_length}{avg\_doc\_length}$, being multiplied by $k$ in the saturation formula. When $b=0$ we will not take into account the document length, and when $b=1$ we will fully take into account the document length.

Formula

Although some modifications were proposed for the IDF part of the formula, the most important changes were described in the assumptions section. The BM25 formula, then, is the following:

$\text{BM25}(t, d) = \frac{\text{TF}(t, d) \times (k_1 + 1)}{\text{TF}(t, d) + k_1 \times (1 - b + b \times \frac{\text{doc\_length}}{\text{avg\_doc\_length}})} \times \log{\frac{\text{total number of documents}}{\text{number of documents containing t}}}$

Problems

• Semantic understanding: The BM25 algorithm does not take into account the semantic understanding of the terms. Cannot distinguish between “cat” and “cats”, for example. To solve this problem we need to use more complex algorithms, like word embeddings, that can capture the semantic meaning of the terms.

Credits

• Understanding TF-IDF and BM-25
• Breaking Down the TF-IDF Formula
• TF-IDF Implementation by Scikit-Learn