VGG - Very Deep Convolutional Networks

To date, convolutional filters of different sizes have been used, such as the AlexNet architecture in which 11×11 or 5×5 filters were used, which made them computationally expensive. The VGGs propose using smaller 3×3 filters that give good results and make networks less costly and computationally affordable, making them deeper.

Main Ideas

The paper addresses an important aspect of ConvNet architecture design – its depth. To this end, authours fix other parameters of the architecture, and steadily increase the depth of the network by adding more convolutional layers, which is feasible due to the use of very small (3×3) convolution filters in all layers.

The proposed network uses very small 3×3 receptive fields throughout the whole net, which are convolved with the input at every pixel (with stride 1). It is easy to see that a stack of two 3×3 convolutional layers (without spatial pooling in between) has an effective receptive field of 5×5; three such layers have a 7×7 effective receptive field. So what have we gained by using, for instance, a stack of three 3×3 convolutional layers instead of a single 7×7 layer? First, incorporates three non-linear rectification layers instead of a single one, which makes the decision function more discriminative. Second, decreases the number of parameters: assuming that both the input and the output of a three-layer 3×3 convolution stack has $C$ channels, the stack is parametrized by $3(3^2C^2)=27C^2$ weights; at the same time, a single 7×7 convolutional layer would require $7^2C^2=49C^2$ parameters, i.e., 81% more. This can be seen as imposing a regularisation on the 7×7 convolutional filters, forcing them to have a decomposition through the 3×3 filters (with non-linearity injected in between). To know more about why use 3×3 and the receptive field go to The Receptive Field in Convolutional Neural Networks.

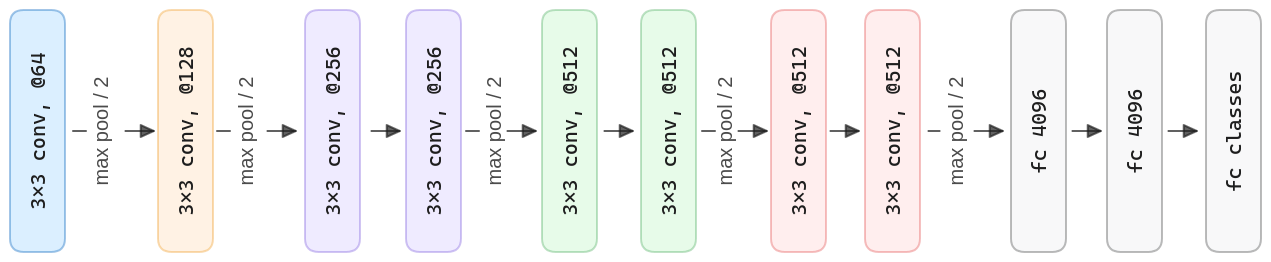
Architecture & Training Details

Regarding the data, the input is a fixed-size 224×224 RGB image. Subtracting each pixel’s mean RGB value, computed on the training set.

For the architecture, the convolutional layers use filters with a small receptive field of 3×3. The convolution stride is fixed to 1 pixel. The padding is 1, so the spatial resolution is preserved after each convolution. To carry out the spatial pooling, max-pooling layers with 2×2 pixel windows and stride two are used. Finally, for the classification, three stacked, fully-connected layers were used.

VGG Configurations. The depth of the configurations increases from the left to the right, as more layers are added (the added layers are shown in bold). The convolutional layer parameters are denoted as conv. The ReLU activation function and the Batch Normalization is not shown for brevity.

VGG Configuration
11 weight layers	13 weight layers	16 weight layers	19 weight layers
input (224×224 RGB image)
conv 3x3 @64	conv 3x3 @64 conv 3x3 @64	conv 3x3 @64 conv 3x3 @64	conv 3x3 @64 conv 3x3 @64
Max Pooling
conv 3x3 @128	conv 3x3 @128 conv 3x3 @128	conv 3x3 @128 conv 3x3 @128	conv 3x3 @128 conv 3x3 @128
Max Pooling
conv 3x3 @256 conv 3x3 @256	conv 3x3 @256 conv 3x3 @256	conv 3x3 @256 conv 3x3 @256 conv 3x3 @256	conv 3x3 @256 conv 3x3 @256 conv 3x3 @256 conv 3x3 @256
Max Pooling
conv 3x3 @512 conv 3x3 @512	conv 3x3 @512 conv 3x3 @512	conv 3x3 @512 conv 3x3 @512 conv 3x3 @512	conv 3x3 @512 conv 3x3 @512 conv 3x3 @512 conv 3x3 @512
Max Pooling
conv 3x3 @512 conv 3x3 @512	conv 3x3 @512 conv 3x3 @512	conv 3x3 @512 conv 3x3 @512 conv 3x3 @512	conv 3x3 @512 conv 3x3 @512 conv 3x3 @512 conv 3x3 @512
Max Pooling
Fully Connected 4096
Fully Connected 4096
Fully Connected Classes
Softmax

Code

First, we import the libraries we are going to use.

from typing import Dict, List, Union
import torch
from torch import Tensor
from torch import nn

All VGG variants have the same structure, the only difference is the number of convolutional layers and the number of channels in each layer. So we can define a dictionary with the configuration of each variant. This dictionary will help us to manage the different configurations and instantiate the networks creating the layers dynamically.

VGG_CFG: Dict[str, List[Union[str, int]]] = {
    "vgg11": [64, "M", 128, "M", 256, 256, "M", 512, 512, "M", 512, 512, "M"],
    "vgg13": [64, 64, "M", 128, 128, "M", 256, 256, "M", 512, 512, "M", 512, 512, "M"],
    "vgg16": [64, 64, "M", 128, 128, "M", 256, 256, 256, "M", 512, 512, 512, "M", 512, 512, 512, "M"],
    "vgg19": [64, 64, "M", 128, 128, "M", 256, 256, 256, 256, "M", 512, 512, 512, 512, "M", 512, 512, 512, 512, "M"],
}

Each VGG variant is composed of a sequence of convolutional layers, max-pooling layers (denoted by M), and finally all variants share the same fully-connected layers structure. So we can define a class that will be the base and will receive the configuration of the convolutional layers:

class VGG(nn.Module):
    """
    A VGG network implementation with customizable configurations.

    Args:
        cfg (str): One of the available VGG configurations: vgg11, vgg13, vgg16, vgg19
        num_classes (int): The number of classes in the classification task.

    Attributes:
        features (nn.Sequential): The convolutional layers of the network.
        maxpool (nn.AdaptiveMaxPool2d): The adaptive max pooling layer.
        classifier (nn.Sequential): The fully connected layers of the network.

    Methods:
        _make_layers(vgg_cfg): Creates convolutional layers based on the input cfg.
        forward(x): Performs a forward pass of the input through the network.
    """
    def __init__(self, cfg: List[Union[str, int]], num_classes: int = 1000) -> None:
        super(VGG, self).__init__()
        self.features = self._make_layers(VGG_CFG[cfg])

        self.maxpool = nn.AdaptiveMaxPool2d((7, 7))

        self.classifier = nn.Sequential(
            # 512 maps of 7x7 pixels -> 224 input / 2M / 2M / 2M / 2M / 2M = 7
            nn.Linear(512 * 7 * 7, 4096),
            nn.ReLU(True),
            nn.Dropout(0.5),
            nn.Linear(4096, 4096),
            nn.ReLU(True),
            nn.Dropout(0.5),
            nn.Linear(4096, num_classes),
        )
        
    def _make_layers(self, vgg_cfg: List[Union[str, int]]) -> nn.Sequential:
        """
        Creates the convolutional layers of the network based on the input configuration.

        Args:
            vgg_cfg (List[Union[str, int]]): A list of integers and strings
                representing the architecture of the network.
                Integers represent the number of output channels
                in the corresponding convolutional layer.
                Strings represent max pooling layers and have the value "M".

        Returns:
            nn.Sequential: A sequential module with the convolutional layers of the network.
        """
        layers: nn.Sequential[nn.Module] = nn.Sequential()
        in_channels = 3
        for v in vgg_cfg:
            if v == "M":
                layers.append(nn.MaxPool2d((2, 2), (2, 2)))
            else:
                conv2d = nn.Conv2d(in_channels, v, (3, 3), (1, 1), (1, 1))
                layers.append(conv2d)
                layers.append(nn.BatchNorm2d(v))
                layers.append(nn.ReLU(True))
                in_channels = v

        return layers

    def forward(self, x: Tensor) -> Tensor:
        """
        Performs a forward pass of the input through the network.

        Args:
            x (Tensor): The input tensor to the network. Shape (batch, 3, 224, 224)

        Returns:
            Tensor: The output tensor from the network. Shape (batch, num_classes)
        """
        out = self.features(x)
        out = self.maxpool(out)
        out = torch.flatten(out, 1)
        out = self.classifier(out)

        return out

The module VGG receives the configuration of the convolutional layers and the number of classes. Then, it creates the convolutional layers using the method _make_layers and the configuration. Finally, it creates the fully-connected layers and the adaptive max pooling layer.

The method _make_layers receives the configuration of the convolutional layers. Then, it creates a sequential module and iterates over the configuration, a list of integers and strings M for max-pooling layers. In each iteration, if the value is M it creates a max-pooling layer with a 2×2 kernel and stride 2, otherwise the value is an integer and it creates a convolutional layer with the number of latest input channels and current output channels, the current value of the iteration. When adding convolutions, it also adds a Batch Normalization layer and a ReLU activation function.

Finally, the method forward receives the input tensor and performs a forward pass through the network. We can simply test our network by calling the following test:

def test():
    """
    Tests the VGG network implementation.

    Instantiates a VGG network object with the 'vgg11' configuration
    and performs a forward pass of a randomly generated input tensor
    through the network. Prints the size of the output tensor.

    """
    net = VGG('vgg11')
    x = torch.randn(2, 3, 224, 224)
    y = net(x)
    print(y.size())
    
test()

Credits

• Paper - Very Deep Convolutional Networks for Large-Scale Image Recognition
• Kuangliu model implementation