ResNet’s main contribution is the introduction of the residual block, which enables the creation of much deeper neural networks without encountering the vanishing gradient problem.
Main Ideas
Deep neural networks are more difficult to train. ResNet authors present a residual learning framework to ease the training of networks that are substantially deeper than those used previously.
When deeper networks are able to start converging, a degradation problem has been exposed: with the network depth increasing, accuracy gets saturated (which might be unsurprising) and then degrades rapidly. Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error.
The paper addresses the degradation problem by introducing a deep residual learning framework. It hypotheses that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping.
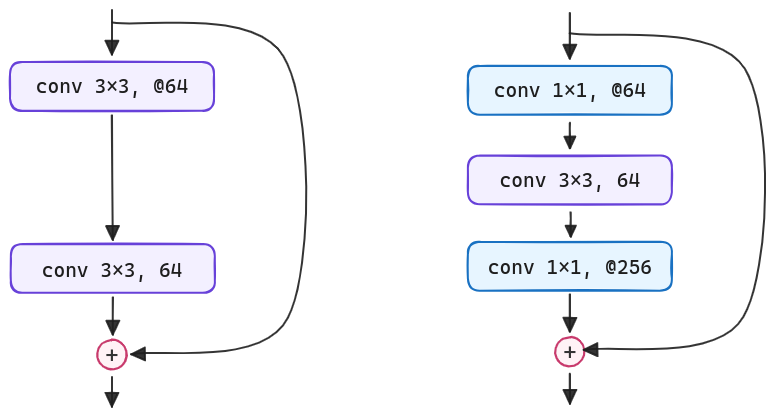
Because of concerns on the trianing time that authors can afford, for deeper nets they modify the base residual building block as a bottleneck design. The bottleneck stacks 1×1, 3×3, and 1×1 convolutions, where the 1×1 layers are responsible for reducing and then increasing (restoring) dimensions, leaving the 3×3 layer a bottleneck with smaller input/output dimensions.
ResNet shows how extremely deep residual nets are easy to optimize, but the counterpart “plain” nets (that simply stack layers as the VGG Network) exhibit higher training error when the depth increases. Deep residual nets can easily enjoy accuracy gains from greatly increased depth, producing results substantially better than previous networks.

Architecture & Training Details
The data is randomly sampled its shorter side in the range [256, 480], then randomly cropped to 224×224. Per-pixel mean subtracted. Standard color augmentation is used. Batch normalization after each convolution, before activation function.
In general terms in the architecture, if the feature map size is halved, the number of filters is doubled. Downsampling directly by convolutional layers that have a stride of 2. Just one fully-connected layer is used. Convolutional layers mostly have 3×3 filters. The learning rate starts from 0.1, using SGD with a weight decay of 0.0001 and momentum of 0.9, no dropout.
| Output size | 18-layer | 34-layer | 50-layer | 101-layer | 152-layer |
|---|---|---|---|---|---|
| 112x112 | 7x7, 64, stride 2, pad 3 | ||||
| 56x56 | 3x3 max pool, stride 2 | ||||
| 28x28 | |||||
| 14x14 | |||||
| 7x7 | |||||
| 1x1 | averge pool + fully connected [classes] + softmax | ||||
Code
Let’s create the main residual block, which we see in Figure 2. Remember that the downsampling is done by applying stride 2 in certain convolutions. When we do the downsampling, the shortcut also uses it to match the reduced dimension and the out channels.
class ResBlock(nn.Module):
def __init__(self, in_channels, out_channels, downsample):
super().__init__()
"""
Args:
in_channels (int): number of input channels
out_channels (int): number of output channels
downsample (bool): if True, downsamples the input
"""
if downsample:
# when downsample is True, the first conv layer of the block has stride=2
# which downsample the input x by a factor of 2. We also need to downsample
# the residual branch, so we use a stride of 2 as well.
self.conv1 = nn.Conv2d(
in_channels, out_channels, kernel_size=3, stride=2, padding=1
)
self.shortcut = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=2),
nn.BatchNorm2d(out_channels)
)
else:
self.conv1 = nn.Conv2d(
in_channels, out_channels, kernel_size=3, stride=1, padding=1
)
self.shortcut = nn.Sequential()
self.conv2 = nn.Conv2d(
out_channels, out_channels, kernel_size=3, stride=1, padding=1
)
self.bn1 = nn.BatchNorm2d(out_channels)
self.bn2 = nn.BatchNorm2d(out_channels)
def forward(self, x):
shortcut = self.shortcut(out)
out = nn.ReLU()(self.bn1(self.conv1(out)))
out = nn.ReLU()(self.bn2(self.conv2(out)))
out = out + shortcut
return nn.ReLU()(out)Below, we show what the 18-layer ResNet, ResNet18, would look like using these residual blocks.
class ResNet18(nn.Module):
def __init__(self, in_channels, resblock, outputs=1000):
super().__init__()
"""
Args:
in_channels (int): number of input channels
resblock (nn.Module): the resblock to use
outputs (int): number of outputs
"""
self.layer0 = nn.Sequential(
nn.Conv2d(in_channels, 64, kernel_size=7, stride=2, padding=3),
nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
nn.BatchNorm2d(64),
nn.ReLU()
)
self.layer1 = nn.Sequential(
resblock(64, 64, downsample=False),
resblock(64, 64, downsample=False)
)
self.layer2 = nn.Sequential(
resblock(64, 128, downsample=True),
resblock(128, 128, downsample=False)
)
self.layer3 = nn.Sequential(
resblock(128, 256, downsample=True),
resblock(256, 256, downsample=False)
)
self.layer4 = nn.Sequential(
resblock(256, 512, downsample=True),
resblock(512, 512, downsample=False)
)
self.gap = torch.nn.AdaptiveAvgPool2d(1)
self.fc = torch.nn.Linear(512, outputs)
def forward(self, x):
x = self.layer0(x)
out = self.layer1(out)
out = self.layer2(out)
out = self.layer3(out)
out = self.layer4(out)
out = self.gap(out)
out = torch.flatten(out)
out = self.fc(out)
return outThe Bottleneck block for ResNet-50/101/152 variants would be as follows:
class ResBottleneckBlock(nn.Module):
def __init__(self, in_channels, out_channels, downsample):
super().__init__()
self.downsample = downsample
self.conv1 = nn.Conv2d(
in_channels, out_channels//4, kernel_size=1, stride=1
)
self.conv2 = nn.Conv2d(
out_channels//4, out_channels//4,
kernel_size=3, stride=2 if downsample else 1, padding=1
)
self.conv3 = nn.Conv2d(
out_channels//4, out_channels, kernel_size=1, stride=1
)
self.shortcut = nn.Sequential()
if self.downsample or in_channels != out_channels:
self.shortcut = nn.Sequential(
nn.Conv2d(
in_channels, out_channels,
kernel_size=1, stride=2 if self.downsample else 1
),
nn.BatchNorm2d(out_channels)
)
self.bn1 = nn.BatchNorm2d(out_channels//4)
self.bn2 = nn.BatchNorm2d(out_channels//4)
self.bn3 = nn.BatchNorm2d(out_channels)
def forward(self, x):
shortcut = self.shortcut(x)
out = nn.ReLU()(self.bn1(self.conv1(out)))
out = nn.ReLU()(self.bn2(self.conv2(out)))
out = nn.ReLU()(self.bn3(self.conv3(out)))
out = out + shortcut
return nn.ReLU()(x)