SENet - Very Deep Convolutional Networks

Squeeze-and-Excitation Networks (SENets) are a type of convolutional neural network (CNN) architecture that introduce a mechanism called channel attention to improve the performance of image classification tasks. The main contributions of SENets can be summarized as follows:

1. Channel attention: The SENet architecture introduces a mechanism called channel attention which learns to emphasize informative features and suppress less useful ones selectively. This is achieved by using a squeeze operation to compress the spatial dimensions of feature maps into a vector, followed by an excitation operation that learns to weight each channel of the feature map based on its importance.
2. Generalization: SENets have been shown to improve generalization performance, allowing them to generalize well to unseen data. This is likely because channel attention helps to filter out noise and irrelevant features, which can help to reduce overfitting.

Main Ideas

SENet investigates a different aspect of network design, the relationship between channels, explicitly modeling the interdependencies between the channels of their convolutional features.

For any given transformation $F_{tr}$ mapping the input $X$ to the feature maps $U$ where $U ∈ R ^{H×W×C}$, e.g. a convolution, we can construct a corresponding SE block to perform feature recalibration. The features U are first passed through a squeeze operation, which produces a channel descriptor by aggregating feature maps across their spatial dimensions (H × W). The function of this descriptor is to produce an embedding of the global distribution of channel-wise feature responses, allowing information from the global receptive field of the network to be used by all its layers. The aggregation is followed by an excitation operation, which takes the form of a simple self-gating mechanism that takes the embedding as input and produces a collection of per-channel modulation weights. These weights are applied to the feature maps U to generate the output of the SE block, which can be fed directly into subsequent layers of the network.

SE blocks are also computationally lightweight and impose only a slight increase in model complexity and computational burden.

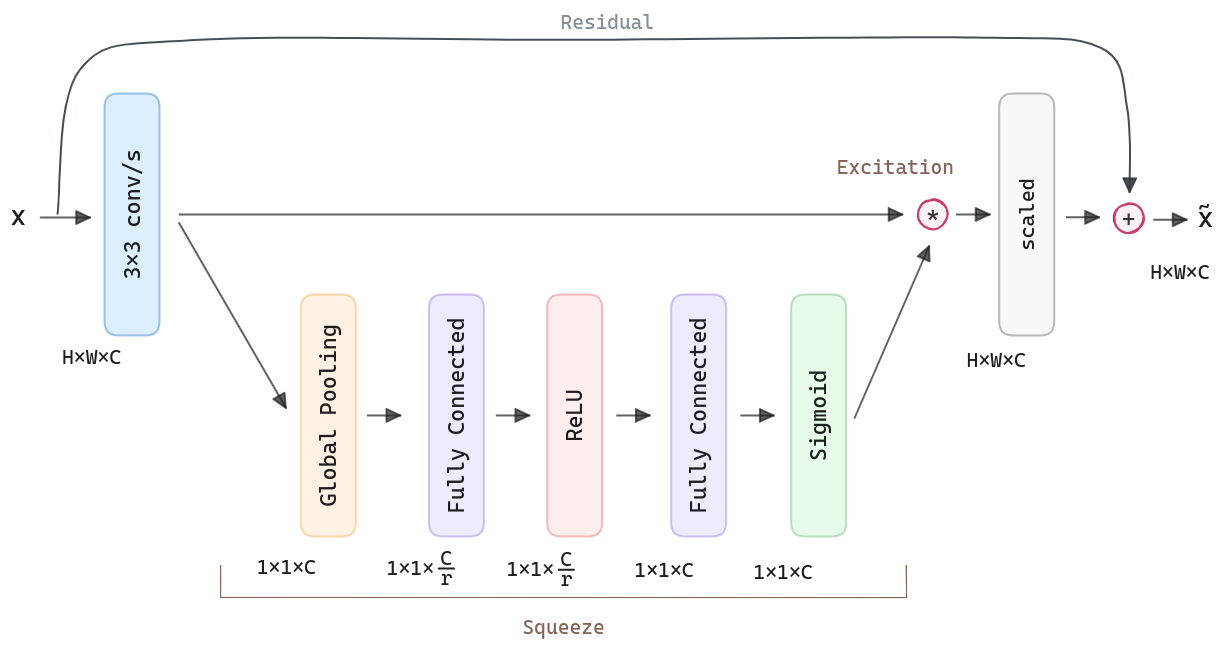
In the convolution, the output is produced by a summation through all channels. Channel dependencies are implicitly embedded but are entangled with the local spatial correlation captured by the filters. We expect the learning of convolutional features to be enhanced by explicitly modeling channel interdependencies so that the network can increase its sensitivity to informative features, which can be exploited by subsequent transformations. To do so, two steps: squeeze and excitation, before they are fed into the next transformation.

Squeeze: Global Information Embedding. Each of the learned filters operates with a local receptive field, and consequently, each unit of the transformation output $U$ is unable to exploit contextual information outside of this region. To mitigate this problem, we propose to squeeze global spatial information into a channel descriptor. This is achieved by using global average pooling to generate channel-wise statistics.

Excitation: Adaptive Recalibration. To make use of the information aggregated in the squeeze operation, we follow it with a second operation that aims to fully capture channel-wise dependencies. To fulfill this objective, the function must meet two criteria:

1. It must be flexible (in particular, capable of learning a nonlinear interaction between channels).
2. It must learn a non-mutually-exclusive relationship since we would like to ensure that multiple channels are allowed to be emphasized (rather than enforcing a one-hot activation).

We opt to employ a simple gating mechanism with sigmoid activation. To limit model complexity and aid generalization, we parameterize the gating mechanism by forming a bottleneck with two fully-connected (FC) layers around the non-linearity, i.e., a dimensionality-reduction layer with reduction ratio $r$, a ReLU and then a dimensionality-increasing layer returning to the channel dimension of the transformation output $U$. The final output of the block is obtained by rescaling $U$ with the activations.

Architecture & Training Details

Authors perform the experiments on the ImageNet 2012 dataset. They follow standard practices and perform data augmentation with random cropping using scale and aspect ratio to a size of 224 × 224 pixel, and perform random horizontal flipping. Each input image is normalised through mean RGB-channel subtraction.

Optimisation is performed using synchronous SGD with momentum 0.9 and a minibatch size of 1024. The initial learning rate is set to 0.6 and decreased by a factor of 10 every 30 epochs. Models are trained for 100 epochs from scratch. The reduction ratio $r$ is set to 16 by default.

Code

Here it is the standard SE block, which uses a residual connection, then the SE output is aggregated to the input.

class SEBlock(nn.Module):
    def __init__(self, in_planes, planes, stride=1, reduction_ratio=16):
        super(SEBlock, self).__init__()
        self.conv1 = nn.Conv2d(
            in_planes, planes,
            kernel_size=3, stride=stride, padding=1, bias=False
        )
        self.bn1 = nn.BatchNorm2d(planes)

        self.conv2 = nn.Conv2d(
            planes, planes,
            kernel_size=3, stride=1, padding=1, bias=False
        )
        self.bn2 = nn.BatchNorm2d(planes)

        self.shortcut = nn.Sequential()
        if stride != 1 or in_planes != planes:
            self.shortcut = nn.Sequential(
                nn.Conv2d(
                    in_planes, planes,
                    kernel_size=1, stride=stride, bias=False
                ),
                nn.BatchNorm2d(planes)
            )

        # SE layers
        self.fc1 = nn.Conv2d(planes, planes//reduction_ratio, kernel_size=1)
        self.fc2 = nn.Conv2d(planes//reduction_ratio, planes, kernel_size=1)

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))

        # Squeeze
        w = F.avg_pool2d(out, out.size(2))
        w = F.relu(self.fc1(w))
        w = F.sigmoid(self.fc2(w))

        # Excitation
        out = out * w

        # Residual connection
        out += self.shortcut(x)
        out = F.relu(out)
        return out

Next, we the SENet architecture can be implemented as follows:

class SENet(nn.Module):
    def __init__(self, num_blocks, num_classes=10):
        super(SENet, self).__init__()
        self.in_planes = 64

        self.conv1 = nn.Conv2d(
            3, 64, kernel_size=3, stride=1, padding=1, bias=False
        )
        self.bn1 = nn.BatchNorm2d(64)
        self.layer1 = self._make_layer(64, num_blocks[0], stride=1)
        self.layer2 = self._make_layer(128, num_blocks[1], stride=2)
        self.layer3 = self._make_layer(256, num_blocks[2], stride=2)
        self.layer4 = self._make_layer(512, num_blocks[3], stride=2)
        self.linear = nn.Linear(512, num_classes)

    def _make_layer(self, planes, num_blocks, stride):
        strides = [stride] + [1]*(num_blocks-1)
        layers = []
        for stride in strides:
            layers.append(SEBlock(self.in_planes, planes, stride))
            self.in_planes = planes
        return nn.Sequential(*layers)

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.layer4(out)
        out = F.avg_pool2d(out, 4)
        out = out.view(out.size(0), -1)
        out = self.linear(out)
        return out

An analogous to ResNet18 can be instantiated as follows:

def SENet18():
    return SENet([2,2,2,2])

Credits

• Paper - Squeeze-and-Excitation Networks